Given, we understand what vectors are from previous blog and what magnitude and direction represent, We will see how to measure the “closeness” or “similarity” between vectors with simple example. Two of the most common metrics are Cosine Similarity and Dot Product. While both are derived from the same mathematical operations, they capture different aspects of similarity and are used in distinct scenarios

Dot Product:

The Dot Product of two vectors is a single number that represents the magnitude of one vector in the direction of the other.

Formula:

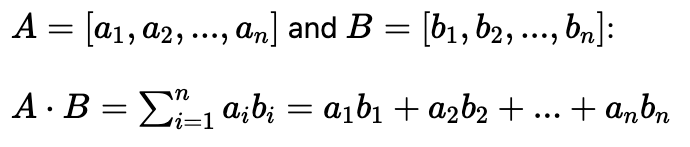
*Note that Python ‘numpy‘ library has function to calculate the Dot Product between 2 vectors.

How to Interpret:

• A large positive dot product means the vectors are pointing in roughly the same direction and both have large magnitudes.
• A large negative dot product means they are pointing in opposite directions and both have large magnitudes.
• A dot product near zero means they are orthogonal (perpendicular) or at least one vector has a small magnitude.

The Dot Product is sensitive to both the direction and the magnitude (length) of the vectors. Longer vectors (representing more “prominent” or “frequent” features) will generally have larger dot products.

Cosine Similarity:

Cosine Similarity measures the cosine of the angle between two vectors. It determines whether two vectors are pointing in roughly the same direction, regardless of their magnitude.

Formula:

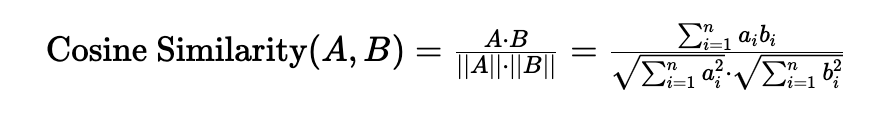
*Note that Python ‘sklearn‘ library has functions to calculate cosine similarity between 2 vectors.

How to Interpret:

• The result ranges from -1 to 1.
• 1 means the vectors are identical in direction
• 0 means the vectors are orthogonal , indicating no similarity.
• -1 means the vectors are diametrically opposed , indicating complete dissimilarity

Cosine Similarity is sensitive only to the direction of the vectors, not their magnitude. It effectively normalizes the vectors to unit length before calculating the dot product.

When to use Dot Product:

• When the “strength” or “prominence” of a feature is important. For example, in recommendation systems where a user’s strong preference for an item (high magnitude in their preference vector) should contribute more to the similarity score.

When to use Cosine Similarity:

• Text Similarity – Most common for comparing documents, sentences, or words. If a document is twice as long but talks about the same topic, its vector might be longer, but its direction (semantic meaning) remains the same. Cosine similarity correctly identifies this.

Example: “Apple” the Fruit vs. “Apple” the Company

Let’s consider a scenario where we have a search query and three different documents. We’ll represent them as 2-dimensional vectors for simplicity, where:

• Dimension 1 represents “fruitiness” concepts.
• Dimension 2 represents “technology” or “corporate” concepts.

The magnitude of the vector can conceptually represent the prominence or frequency of the concept in a document.

Query: “I want to buy a new phone from Apple.”

Query Vector (Q): [0.3, 0.7] (Slightly more tech-oriented, as it’s about a phone from Apple)

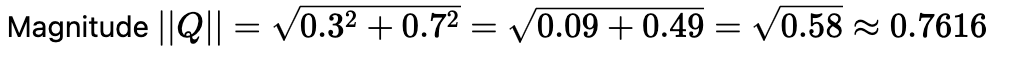
Document Vectors:

1. Document A (Fruit Context):

“I ate a delicious apple today. It was very sweet.”

Vector A (V_fruit_apple): [0.9, 0.1] (High fruitiness, low tech. Normal prominence.)

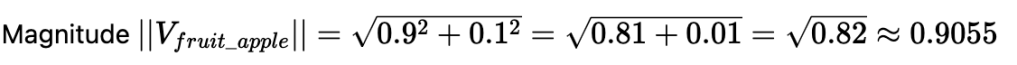
2. Document B (Company Context, Normal Mention):

“Apple released a new iPhone today. The stock went up.”

Vector B (V_company_apple_normal): [0.2, 0.8] (Low fruitiness, high tech. Normal prominence.)

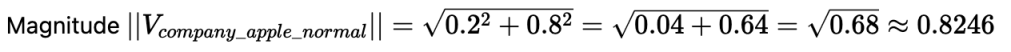
3. Document C (Company Context, Prominent Mention):

” Apple. Apple Inc. The tech giant Apple announced record earnings.”

Vector C (V_company_apple_prominent): [0.4, 1.6] (Same direction as ‘V_company_apple_normal’, but twice the magnitude, implying higher prominence/frequency of the company concept.)

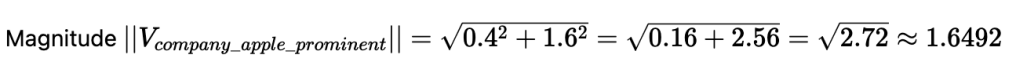
Calculations and Interpretation:

1. Query (Q) vs. Document A (V_fruit_apple)

Dot Product:

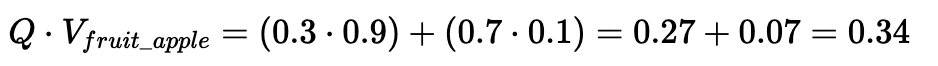
Cosine Similarity:

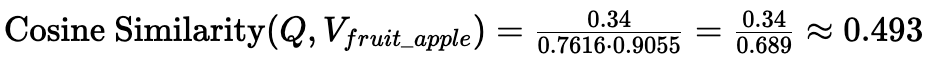
Interpretation: Both metrics show low similarity. The query is tech-focused, while Document A is about fruit.

2. Query (Q) vs. Document B (V_company_apple_normal)

Dot Product:

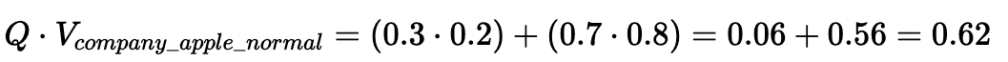
Cosine Similarity:

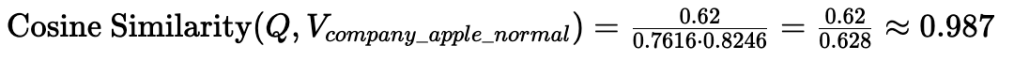
Interpretation: Both metrics show high similarity. Document B is clearly about Apple the company, matching the query’s intent.

3. Query (Q) vs. Document C (V_company_apple_prominent)

Dot Product:

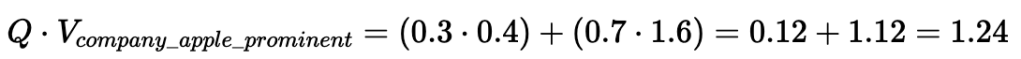
Cosine Similarity:

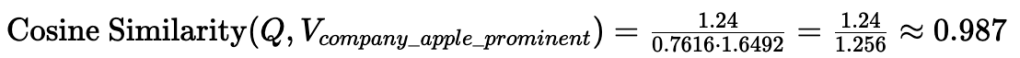
Interpretation:

Cosine Similarity remains high (0.987), identical to Document B. This is because Document C’s vector points in the exact same semantic direction as Document B’s, even though it’s longer. Cosine Similarity correctly identifies that both documents are equally relevant to “Apple the company” semantically.

Dot Product is significantly higher for Document C(1.24) than for Document B (0.62). This is because the Dot Product considers the larger magnitude of Document C’s vector. If prominence or frequency of mention is important (e.g., a document that talks a lot about “Apple” is more relevant), then Dot Product captures this.

---

Takeaways:

• Cosine Similarity is ideal when you care primarily about the semantic meaning or topic similarity, regardless of how prominently or frequently a concept is mentioned. It tells you if two vectors are pointing in the same direction.
• Dot Product is useful when both semantic similarity AND the prominence/magnitude of the vectors are important. A higher dot product can indicate not just semantic alignment but also a stronger presence or relevance of the concept.